A major hurdle for quantum algorithms for linear systems of equations, and for quantum simulation algorithms, is the difficulty to find simple circuits for arithmetic. Prior approaches typically led to a large overhead in terms of quantum memory, required operations, or implementation error.
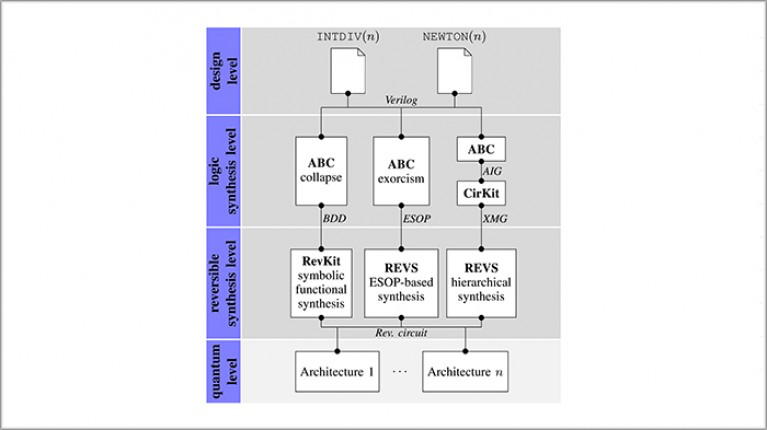
By leveraging recent advances in reversible logic synthesis, Martin Roetteler and Nathan Wiebe (both QuArC), together with Mathias Soeken and Giovanni De Micheli (both EPFL), synthesized highly optimized arithmetic circuits using classical design automation flows and tools. The combination of classical and reversible logic synthesis enables the automatic design of large components in reversible logic, starting from well-known hardware description languages such as Verilog. The tools developed by the authors enable quantum algorithm designers to incorporate a large body of existing conventional logic synthesis software into the quantum realm.
Details of the study are presented in the paper, Design Automation and Design Space Exploration for Quantum Computers, which has been accepted for publication in the proceedings of DATE 2017 (Design, Automation and Test in Europe conference), in March 2017.
As a prototype example, the authors automatically generated high-quality networks for the reciprocal 1/x, which is necessary for quantum linear systems algorithms. You can download all synthesized networks at https://msoeken.github.io/reciprocal.html.
Read the full paper.
